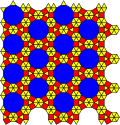
Полурегулярная мозаика
Полурегулярная мозаика[1] — евклидова мозаика, замощающих плоскость двумя или более правильными многоугольниками. Разные авторы перечисляют различные наборы мозаик. Наиболее систематический подход, рассматривающий орбиты симметрии, относится к 2-однородным мозаикам, которых 20. Некоторые из полурегулярных мозаик, фактически, являются 3-однородными мозаиками.
20 2-однородных мозаик
[править | править код]Грюнбаум и Шепард перечислили все 20 2-однородных мозаик в книге Tilings and Paterns (Мозаики и узоры, 1987)[2]:
cmm, 2*22 (44; 33.42)1 |
cmm, 2*22 (44; 33.42)2 |
pmm, *2222 (36; 33.42)1 |
cmm, 2*22 (36; 33.42)2 |
cmm, 2*22 (3.42.6; (3.6)2)2 |
pmm, *2222 (3.42.6; (3.6)2)1 |
pmm, *2222 ((3.6)2; 32.62) |
p4m, *442 (3.12.12; 3.4.3.12) |
p4g, 4*2 (33.42; 32.4.3.4)1 |
pgg, 2× (33.42; 32.4.3.4)2 |
p6m, *632 (36; 32.62) |
p6m, *632 (36; 34.6)1 |
p6, 632 (36; 34.6)2 |
cmm, 2*22 (32.62; 34.6) |
p6m, *632 (36; 32.4.3.4) |
p6m, *632 (3.4.6.4; 32.4.3.4) |
p6m, *632 (3.4.6.4; 33.42) |
p6m, *632 (3.4.6.4; 3.42.6) |
p6m, *632 (4.6.12; 3.4.6.4) |
p6m, *632 (36; 32.4.12) |
Список Гика (1946)
[править | править код]Гика перечислил 10 мозаик с 2 или 3 типами вершин, назвав их полуправильными полиморфными разбиениями[3].
|
|
|
| ||
| Иллюстрация XXVII № 12 4.6.12 3.4.6.4 |
№ 13 3.4.6.4 3.3.3.4.4 |
№ 13 bis. 3.4.4.6 3.3.4.3.4 |
№ 13 ter. 3.4.4.6 3.3.3.4.4 |
Иллюстрация XXIV № 13 quatuor. 3.4.6.4 3.3.4.3.4 |
|
|
| |||
| № 14 33.42 36 |
Иллюстрация XXVI № 14 bis. 3.3.4.3.4 3.3.3.4.4 36 |
№ 14 ter. 33.42 36 |
№ 15 3.3.4.12 36 |
Иллюстрация XXV № 16 3.3.4.12 3.3.4.3.4 36 |
Список Штейнгауза (1969)
[править | править код]Штейнгауз дал 5 примеров негомогенных мозаик из правильных многоугольников, кроме 11 правильных и полуправильных мозаик[4] (все они имеют 2 типа вершин, за исключением одной, являющейся 3-однородной).
| 2-однородные | 3-однородные | |||
|---|---|---|---|---|
|
|
|
|
|
|
| Image 85 33.42 3.4.6.4 |
Image 86 32.4.3.4 3.4.6.4 |
Image 87 3.3.4.12 36 |
Image 89 33.42 32.4.3.4 |
Image 88 3.12.12 3.3.4.12 |
Список Критчлоу (1970)
[править | править код]Критчлоу обнаружил 14 полурегулярных замощений, из которых 7 являются 2-однородными, а 7 — 3-однородными [5].
Он закодировал буквами названия типов вершин с верхним индексом, отражающим порядок грани. Он обнаружил, что вершины типа A, B, C, D, F и J не могут быть частью замощения, покрывающего всю плоскость. В таблице ниже
- (none) означает невозможность присутствия в замощении
- (semi) – получающаяся мозаика полуправильна
- (demi) – получающаяся мозаика полурегулярна
- (reg) – получающаяся мозаика является правильной
| A (none) |
B (none) |
C (none) |
D (none) |
E (semi) |
F (none) |
G (semi) |
H (semi) |
J (none) |
K (2) (reg) | |
|---|---|---|---|---|---|---|---|---|---|---|
 3.7.42 |
 3.8.24 |
 3.9.18 |
 3.10.15 |
 3.12.12[англ.] |
 4.5.20 |
 4.6.12[англ.] |
 4.8.8 |
 5.5.10 |
 63 | |
| L1 (demi) |
L2 (demi) |
M1 (demi) |
M2 (semi) |
N1 (demi) |
N2 (semi) |
P (3) (reg) |
Q1 (semi) |
Q2 (semi) |
R (semi) |
S (1) (reg) |
 3.3.4.12 |
 3.4.3.12 |
 3.3.6.6 |
 3.6.3.6 |
 3.4.4.6 |
 3.4.6.4[англ.] |
 44 |
 3.3.4.3.4 |
 3.3.3.4.4[англ.] |
 3.3.3.3.6 |
 36 |
| 1 | 2 | 4 | 6 | 7 | 10 | 14 |
|---|---|---|---|---|---|---|
| 100px]] (3.12.12; 3.4.3.12) |
(36; 32.4.12) |
(4.6.12; 3.4.6.4) |
((3.6)2; 32.62) |
(3.4.6.4; 32.4.3.4) |
(36; 32.4.3.4) |
(3.4.6.4; 3.42.6) |
| E+L2 | L1+(1) | N1+G | M1+M2 | N2+Q1 | Q1+(1) | N1+Q2 |
| 3 | 5 | 8 | 9 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|
| (3.3.4.3.4; 3.3.4.12, 3.4.3.12) | (36; 3.3.4.12; 3.3.4.3.4) | (3.3.4.3.4; 3.3.3.4.4, 4.3.4.6) | (36, 3.3.4.3.4) | (36; 3.3.4.3.4, 3.3.3.4.4) | (36; 3.3.4.3.4; 3.3.3.4.4) | (3.4.6.4; 3.42.6) |
| L1+L2+Q1 | L1+Q1+(1) | N1+Q1+Q2 | Q1+(1) | Q1+Q2+(1) | Q1+Q2+(1) | N1+N2 |
Примечания
[править | править код]- ↑ В английском языке используется два слова — demiregular и semiregular, оба слова на русский можно перевести как полуправильные. Для различения этих понятий будем называть semiregular tilings полуправильными мозаиками, а demiregular tilings — полурегулярными.
- ↑ Grünbaum, Shephard, 1987, с. 65.
- ↑ Ghyka, 1977, с. 73-80.
- ↑ Steinhaus, 1969, с. 79-82.
- ↑ Critchlow, 1987, с. 62-67.
Литература
[править | править код]- M. Ghyka. The Geometry of Art and Life. — 2nd. — New York: Dover, 1977. Переиздание, книги 1946 года.
- Keith Critchlow. Order in Space: A design source book. — New York: Thames & Hudson, 1987. — ISBN 0-500-34033-1.
- Robert Williams. The Geometrical Foundation of Natural Structure: A Source Book of Design. — Dover Publications, Inc, 1979. — С. 35-43. — ISBN 0-486-23729-X.
- H. Steinhaus. Mathematical Snapshots. — 3rd. — Oxford University Press, 1969.Переиздание: 1999, New York, Dover
- Branko Grünbaum, G. C. Shephard. Tilings and Patterns. — W. H. Freeman, 1987. — С. 65. — ISBN 0-7167-1193-1.
- D. Chavey. Tilings by Regular Polygons—II: A Catalog of Tilings // Computers & Mathematics with Applications. — 1989. — Т. 17. — С. 147–165. — doi:10.1016/0898-1221(89)90156-9.
- In Search of Demiregular Tilings, Helmer Aslaksen
Ссылки
[править | править код]- Weisstein, Eric W. Demiregular tessellation (англ.) на сайте Wolfram MathWorld.
- n-uniform tilings Brian Galebach
 | На эту статью не ссылаются другие статьи Википедии. |
| Для улучшения этой статьи желательно:
|