Обсуждение:Комплексное число/Архив/5
Рецензирование[править код]
Ребята какой плахой человек написал формулу умножения комплексных чисел не правильно, знак минуса не в тех скобках. Исправьте кто нибудь. 176.8.130.87 10:57, 4 января 2012 (UTC)
- Проверил. Все знаки на своём месте, плохих людей не обнаружено. LGB 12:12, 4 января 2012 (UTC)
- Всё верно, ошибок нет. --golddim(О|В) 12:29, 4 января 2012 (UTC)
формализм комплексных чисел на сегодня недостаточно проработан[править код]
Вообще формализм комплексных чисел на сегодня недостаточно проработан. Это и демонстрируется в примере неверного использования записи: -1=i^2=sqrt(-1)*sqrt(-1)=sqrt((-1)*(-1))=sqrt(1)=1. Временное решение этой проблемы - предложение записывать sqrt(-3) в современной форме i*sqrt(3) выглядит как залатывание дыр. Если мы обратимся к геометрической интерпретации комплексного числа как точки на комплексной плоскости, то увидим, что и знак "-", относящийся к действительной координате, и знак "-" - в комплексной части имеют различный смысл. В случае со знаком "-" перед мнимой частью речь идет о комплексной сопряженности, а не отрицании самого числа. В случае со знаком "-" перед действительной частью - просто о сопряженности (следует все же различать эти термины). Соответственно, в случае полного отрицания комплексного числа знак "-" ставится как перед действительной, так и перед комплексной частью. Какие будут возражения?91.196.178.5 23:30, 7 июля 2012 (UTC)
- Ваши туманные рассуждения о знаках, извините, не понял, и какое отношение они имеют к предмету обсуждения, тоже для меня загадка. В любом случае не могу согласиться с тем, что современный формат записи комплексного числа (a + b i) есть «временное решение проблемы» и «залатывание дыр». Как теория, так и практика доказали обратное — никаких парадоксов этот формат не вызывает и не может вызвать. Если, конечно, не пользоваться понятием (и свойствами) арифметического корня, который для комплексных чисел не имеет смысла. Так что это решение окончательное и для его пересмотра нет оснований. LGB 10:31, 8 июля 2012 (UTC)
Происхождение мнимой единицы[править код]
Запись корень квадратный из -2, из -3 не делается не потому, что это приводит к ошибкам, что всем понятно. По сути дела здесь поднимается другой вопрос. Только ли возможностью решить уравнение n- степени вводится мнимая единица в математике? Числа Ферма показывают, что это связано с двойственностью числа 1, благодаря которой я решил задачу чисел Ферма частично. Здесь имеется ввиду расположение чисел Ферма на плоскости(скатерть Ветчинникова). Геннадий Ветчинников 14:13, 23 сентября 2012 (UTC)
- Если у Вас опубликована работа на эту тему (в серьёзном журнале) и если она имеет отношение к теме данной статьи, дайте соответствующую ссылку на журнал и можете дополнить статью. Если публикации отсутствуют, правила Википедии запрещают обсуждать предложенную тему, Википедия:НЕФОРУМ. LGB 15:43, 23 сентября 2012 (UTC)
Давно обсуждавшаяся доработка[править код]
В прошлом году обсуждались варианты улучшения статьи, но воз и ныне там. Предлагаю сдвинуть его, и для начала разнести разделы Определение и Обоснование. В качестве основы для первого можно взять ранее согласованный вариант:
Комплексные числа — алгебраическое расширение поля вещественных чисел, содержащее корни всех многочленов с вещественными коэффициентами. Обозначается буквой . В частности, множество содержит число, обычно обозначаемое буквой которое является корнем уравнения
и называется мнимой единицей. Из вида определяющего многочлена следует, что
Арифметические операции, заданные для вещественных чисел, можно распространить на все комплексные числа, превратив множество комплексных чисел в поле. Тогда каждое комплексное число z может быть записано в виде суммы:
где и — вещественные числа. При этом:
- число называется вещественной частью комплексного числа и обозначается или ;
- число называется мнимой частью комплексного числа и обозначается или .
Таким образом, каждое комплексное число может рассматриваться как упорядоченная пара (комплекс) вещественных чисел, откуда и проистекает название «комплексные числа».
Каждое комплексное число вида , у которого отсутствует (равна нулю) мнимая часть, естественным образом отождествляется с вещественным числом В частности, комплексный нуль играет ту же роль, что и вещественный. Комплексное число вида , у которого отсутствует (равна нулю) вещественная часть, называется чисто мнимым и коротко записывается в виде .
Второй раздел (Обоснование) должен содержать описание всех 3 моделей КЧ (включая поле классов вычетов по модулю многочлена , пока что его описание в статье отсутствует) и тем самым доказательство её непротиворечивости. Приглашаю всех конструктивно высказаться по поводу предлагаемых доработок. Если дело пойдёт, можно осуществить и другие обсуждавшиеся в 2011 году планы. LGB 16:04, 31 октября 2012 (UTC)
- На мой взгляд, фраза "алгебраическое расширение поля вещественных чисел, содержащее корни всех многочленов с вещественными коэффициентами." требует толкования (расшифровки) и потому не должна быть первой в этой статье. Я лично её не очень понимаю. Чтобы её понять, мне придётся сходить по ссылкам, которые слава богу в ней есть, и попытаться сформировать в голове совокупность четырёх статей, которые к тому же не особо заботятся об облегчении формирования ровно этой совокупности, да ещё и понять, чем так важны эти "многочлены", что на них тут ссылаются... Ведь, казалось бы, мало ли чего содержит "поле", кроме этих корней.. не понятно, зачем эта фраза именно на корнях акцентируется. В этой фразе, кажется, можно написать "содержащее число 3492806" и осмысленность её не изменится. Что предлагаю по ней: раскрыть сразу на месте в ней все сложные понятия, сократить неизбежно образующиеся при этом излишества, и слово "содержащее" заменить на что-то типа "позволяющее формально конструировать все" - то есть, дать намёк на то, что множество вещественных чисел расширено мнимой единицей именно затем, что такое минимальное добавление позволяет, не меняя всей остальной формальной математики многочленов, получать корней у многочлена всегда столько, какова максимальная степень переменной у этого многочлена, а не говорить, что части корней у некоторых многочленов нет. --Nashev 10:09, 15 февраля 2013 (UTC)
- ...содержащее корни всех многочленов с вещественными коэффициентами... - не совсем правильно, можно подумать, что не содержит корни полиномов с комплексными коэффициентами, поэтому, дескать, нужно вводить новые числа. Мы же знаем, что это не так. Там же упомянуть про основную теорему алгебры. см. re by Nashev.
- Коллега LGB предлагает: ...Второй раздел (Обоснование) должен содержать описание всех 3 моделей КЧ (включая поле классов вычетов по модулю многочлена ..., снова увлечение строгостью, повторюсь, ни математик, ни физик эту статью для самообразования читать не будет, и так знают. Статья для ознакомления. Начинающий должен еще для понимания, теорию вычетов изучить? Может, сразу тут же ТФКП? Риторические вопросы.
- Д.Ильин 12:15, 15 февраля 2013 (UTC).
Я поискал в разных источниках определения КЧ, чтобы знать, на что опереться. Вот результаты.
БСЭ.
Комплексное число — число вида , где — действительные числа, — мнимая единица (число, квадрат которого равен -1).
Математическая энциклопедия.
Алгебраическая природа к. ч. состоит в том, что к. ч. есть элемент (алгебраического) расширения поля действительных чисел R, получаемого алгебраическим присоединением к полю R корня многочлена .
Нечаев В. И. Числовые системы (аналогичное определение даёт Фаддеев, Лекции по алгебре. ).
Под системой комплексных чисел понимают минимальное поле, которое является расширением поля действительных чисел и в котором есть элемент с условием .
Арнольд И. В. Теоретическая арифметика
Всякий комплексный оператор… представляющий объединение в одну двух операций: растяжения и поворота, и задаваемый соответственно парой действительных чисел , мы будем называть комплексным числом.
Ну и т. д. Можно констатировать, что большинство источников так или иначе связывает суть комплексного числа с введением мнимой единицы. Остаётся решить, как этот факт сформулировать. С одной стороны, как я ниже писал и как правильно подчеркнул коллега Nashev, текст должен быть понятен школьнику. С другой стороны, более продвинутых читателей может заинтересовать следующий уровень истины, так что ограничение школьным уровнем стало бы обеднением содержания статьи.
Как всё это совместить? Я думаю, надо в начале текста держаться школьного уровня, подробно разъясняя все возможные трудности, а в конце поместить более элитный материал: КЧ в общей алгебре, Обоснование непротиворечивости КЧ через модели, кратко о комплексных функциях, комплексном анализе и их применении и т. д.
С учётом замечаний коллег предлагаю следующий вариант определения в преамбуле:
Комплексные числа — числовая система, которая получается присоединением к вещественным числам нового, отсутствующего среди вещественных, числа, квадрат которого равен . Это новое число традиционно обозначается буквой и называется мнимой единицей. Каждое комплексное число может быть записано в виде , где — вещественные числа, — мнимая единица.
Далее первым разделом пойдёт определение операций с КЧ.
Что скажете? LGB 17:11, 15 февраля 2013 (UTC)
- Мне в этом варианте не хватает ответа на вопрос «зачем?», и кажется многовато подробностей в ответе на вопрос «что?». На вопросы «что?» и «зачем?» мне хватило бы такого: «Множество комплексных чисел — это множество, получающееся дополнением множества вещественных чисел R мнимой единицей i и содержащими её суммами и произведениями вещественных чисел вида a + ib, что позволяет, не меняя всей остальной формальной математики многочленов, получать корней у многочленов всегда столько, какова максимальная степень переменной у этих многочленов, а не говорить, что части корней у некоторых многочленов нет.». Но это, несомненно, махровый ОРИСС… --Nashev 12:53, 16 февраля 2013 (UTC)
- Термин «множество» интуитивно общепонятен, но для первого определения мне кажется более подходящим нейтральный термин «система». Впрочем, это не принципиально. У Вашего определения 2 недостатка: не упоминается важнейшее свойство мнимой единицы (лезть по гиперссылке из определения — дурной тон), а также упоминаются суммы и произведения, хотя об операциях с КЧ ещё ни слова не сказано. В моём варианте — это пока ещё формальная запись, и только в следующем разделе она раскрывается как сумма. Фраза «что позволяет» и т. д. к определению не относится и более уместна в комментарии к нему (как уже сделано в текущем тексте). LGB 17:48, 16 февраля 2013 (UTC)
- А ещё я тут заметил, что поля, их расширение, алгебраическая замкнутость — это всё понятия, являющиеся особенностями манипулирования многочленами, то есть фактически не самостоятельные и базовые, а имеющие смысл лишь в контексте исследования многочленов. То есть, все статьи про них, с учётом прицела на неспециалистов, было бы уместно начинать с упоминания той области математики, в которой они имеют смысл — с упоминания исследования многочленов. Я прав? --Nashev 12:53, 16 февраля 2013 (UTC)
- Многочлены действительно очень важны для общей теории алгебраических расширений, но с темой данной статьи они соприкасаются лишь в нескольких вторичных точках. Кроме упоминания основной теоремы алгебры, не вижу, что ещё по этой части настолько важно, что заслуживает включения в преамбулу. LGB 17:48, 16 февраля 2013 (UTC)
- Кстати, у вещественных чисел тоже интересное определение:
Веще́ственное, или действи́тельное число — математическая абстракция, возникшая из потребности измерения геометрических и физических величин окружающего мира, а также проведения таких операций как извлечение корня, вычисление логарифмов, решение алгебраических уравнений
.
- По аналогии, для комплексных можно сконструировать определение в таком же духе: «Комплексное число — математическая абстракция, возникшая из потребности проведения таких операций как извлечение корня многочлена…» --Nashev 12:53, 16 февраля 2013 (UTC)
- Это не определение КЧ, а указание их исторического источника. Однако после определения эта фраза была бы, думаю, вполне на месте, она короткая и по существу. LGB 17:48, 16 февраля 2013 (UTC)
- Просмотрел определения КЧ в др. яз. разд. ВП. 2 подхода: 1. i вводится как кв. кор. из -1. 2. Неразрешимость ур-ния x^2+1=0 в вещественных числах. Назову, 1-й - абстрактно-математический, 2-й практический. Совместить бы оба подхода в нашей преамбуле...
- Наиболее близко мне от LGB:
Комплексные числа — числовая система, которая получается присоединением к вещественным числам нового, отсутствующего среди вещественных, числа, квадрат которого равен . Это новое число традиционно обозначается буквой и называется мнимой единицей. Каждое комплексное число может быть записано в виде , где — вещественные числа, — мнимая единица.
- Все хорошо, только... Можно подумать, есть множество вещественных чисел, к нему прибавили 1 элемент i и... все алгебр. ур-ния решаемы? Полезно добавить про аналитические продолжения ф-ций, не только про алг. ур-ния. В электротехнике i, традиционно же, обозначается j.
- Д.Ильин 14:26, 16 февраля 2013 (UTC).
- Просмотрел определения КЧ в др. яз. разд. ВП. 2 подхода: 1. i вводится как кв. кор. из -1. 2. Неразрешимость ур-ния x^2+1=0 в вещественных числах. Назову, 1-й - абстрактно-математический, 2-й практический. Совместить бы оба подхода в нашей преамбуле...
- Я уже выше писал, что об операциях в определении говорить ещё преждевременно. Я специально сформулировал свой вариант так, чтобы было понятно: присоединяется не только мнимая единица, но гораздо больше чисел, подробности должны быть изложены чуть позже. Про особенности электротехники, безусловно, будет упомянуто LGB 17:48, 16 февраля 2013 (UTC)
- В определении и о представлении в виде пары чисел говорить преждевременно. --Nashev 20:44, 6 апреля 2013 (UTC)
Итого: Я начитался Клайна, и в итоге у меня вышел вот такой вариант, ныне текущий. Надеюсь, он всех устроит, и его будут лишь развивать, но не откатывать. --Nashev 20:44, 6 апреля 2013 (UTC)
Для чего, вообще, эта статья!?[править код]
Ещё раз вдумчиво прочёл статью. Я понял всё, что в ней написано. И всё в ней, казалось бы, написано правильно. Но! Я помню смесь ужаса и недоумение когда я впервые её октрыл. Это было на первом курсе и чтобы я тогда (когда мне это было особенно нужно) что-нибудь понял!
С чего начинается статья?
«Комплексные числа — это расширение поля вещественных чисел...»
Кто основная аудитория этой статьи?
Основная аудитория — это школьники старших классов и студенты младших курсов, которые понятия не имеют что такое «поле» (в математическом смысле) вообще и «поле вещественных чисел» в частности. Для чего это вообще там написано?
Эта стать должна давать представление о комплексном числе тем, кто никогда ничего о нём не слышал!
Сейчас же это статья, написанная математиками для математиков.
А теперь о деле. Что, по моему мнению, быть там должно:
Комплексные числа — это множество упорядоченных пар вещественных чисел таких, что .
Заданы две операции:
Здесь можно написать про мнимую единицу:
-
- — называется мнимой единицей
-
-
Далее можно написать про алгебраическую форму комплексного числа:
Далее можно ввести комплексную плоскость:
И показать откуда берётся тригонометрическая форма:
Если найти нормальную картинку, то можно показать почему
и получим:
иначе
умножение
И, наконец, экспоненциальная форма:
Рассмотрим :
Следовательно - показательная функция, так как так себя ведёт показательная функция .
Продифференцируем
Следовательно
Значит
И мы получили знаменитую формулу Эйлера.
Вот необходимый минимум информации, который, по моему мнению, должна содержать эта статья.
А теперь решайте для чего эта статья: для того чтобы потешить самолюбие тех, кто это и так знает, или для того чтобы действительно научить кого-то тому чего он пока не знает.
P.S. Сам бы переписал статью, но она защищена.
- Совершенно согласен с Вами, коллега. Для начинающих подавляющее число математических статей — темный лес. Например, Группа, Кольцо, Неприводимые полиномы, Конечное поле и мн. др. Авторы, увлекшись, забывают для кого пишут статьи. Математики/физики не пользуются такими статьями для изучения, и так всё знают. Начинающим — статьи недоступны пониманию. Следовательно — бесполезны.
- Приветствую Ваш порыв переписать статью в предложенном Вами выше стиле, я его одобряю. Осмелюсь посоветовать — перепишите в инкубаторе, или, зарегистрировавшись, в своей дополнительной странице. Затем, когда будет готово, привлечите внимание коллег. Здесь не сплошь интеллектуальные снобы, весьма вероятно, что после обсуждения Вашего труда Ваш вариант займет достойное место в ОП.
- С уважением, Д.Ильин 08:13, 14 февраля 2013 (UTC).
- Согласен, что нужно упрощать - но!
- Приведённый Вами сплошной массив формул с редкими вкраплениями слов так же ужасен для начинающих, как и сложная терминология.
- Ссылки (как гипертекстовых, так и просто текстовых) на связанные понятия высшей математики в этой статье так же необходимы.
- Эта статья энциклопедическая, и должна содержать исчерпывающую информацию по предмету в заголовке. И это всё же не учебник. --Nashev 15:00, 14 февраля 2013 (UTC)
Согласен с некоторыми обвинениями: во многих математических статьях царит дикий и неоправданный выпендрёж, делающий их бесполезными для читателя. Скажем, Дифференциальный оператор, Конформное отображение и легион других. Нельзя тупо переписывать в Википедию статьи из Мат. энциклопедии, рассчитанной совсем на другой контингент читателей. Конечно, Википедия не учебник, но каждая статья должна быть способна дать неспециалисту (минимально соответствующего уровня) первоначальное представление о своём предмете. Это уже обсуждалось, см. ВП:Специализированные статьи должны быть понятны, но пока никаких мер не принято.
С другой стороны, предлагаемая куча формул ещё хуже, чем текущий вариант, так как не содержит важнейшего для новичков пункта — идеологии, то есть описания полезности комплексных чисел, практических указаний на то, где, зачем и благодаря чему они нужны в науке, пояснений, как с ними надо (и не надо) обращаться. Определение КЧ как «пары чисел» вообще неприемлемо, об этом уже шёл спор пару лет назад. Комплексное число — это не «пара чисел»! Не надо принимать наглядное представление (модель) за суть КЧ.
Я давно собираюсь заняться данной статьёй, но что-то никто не откликнулся на мою реплику от октября 2012 года. Может, приступим? Для начала согласуем определение КЧ в преамбуле, оно должно быть максимально простым и основанным на истинной сути КЧ: добавлению к системе вещественных чисел мнимой единицы. И исторически, и методологически это главный пункт, модель Гамильтона с парами чисел появилась на 200 лет позже. LGB 16:07, 14 февраля 2013 (UTC)
- Тогда уж в преамбуле - историю появления понятия КЧ - к Кардано, напр., корни полинома, разрешимого в радикалах: x(x+1)(x-1) с 3 вещественными корнями, которые не могут быть найдены без идеи квадратного корня из -1. Д.Ильин 12:56, 15 февраля 2013 (UTC).
- Исторический раздел надо расширить, причём, кроме Кардано, подробнее рассказать об открытиях Бомбелли, только почему в преамбуле? LGB 16:30, 15 февраля 2013 (UTC)
- Коллега LGB, преамбула - деликатна. С одной стороны, - не выплеснуть бы ребенка с водой из ванны, с другой - слона бы в нее не затащить. Думаю, в преамбуле обязательно упор на историю, почему нужны стали КЧ - потребность практики. Нашим полуживотным предкам хватало натуральных чисел, далее - рациональные и т.д. Там же - основную теорему алгебры и аналитическое продолжение неразрешимых в вещественных числах функций при НДЗ в вещественных числах аргументов, напр. ln(x) при x<0. И только потом a+ib.
- Я сторонник наращивания сложности изложения сверху-вниз. Иначе, если сразу сложно, читатель бросает читать. Что касается строгостей по Гамильтону и др. определений - то в самый конец, для продвинутых.
- С уважением, Д.Ильин 17:36, 15 февраля 2013 (UTC).
- Коллега LGB, преамбула - деликатна. С одной стороны, - не выплеснуть бы ребенка с водой из ванны, с другой - слона бы в нее не затащить. Думаю, в преамбуле обязательно упор на историю, почему нужны стали КЧ - потребность практики. Нашим полуживотным предкам хватало натуральных чисел, далее - рациональные и т.д. Там же - основную теорему алгебры и аналитическое продолжение неразрешимых в вещественных числах функций при НДЗ в вещественных числах аргументов, напр. ln(x) при x<0. И только потом a+ib.
- В случае реализации всего Вами перечисленного преамбула займёт четверть, а то и треть статьи. Согласно ВП:Преамбула и Википедия:Преамбула/перевод, «Преамбула — вводная часть статьи, содержащая определение предмета статьи и её краткий пересказ»; «Подробное изложение уместно в тексте статьи, но не в преамбуле». Задача преамбулы — очертить предмет статьи и вызвать интерес читателя. Аналитическое продолжение и упор на историю скорее читателя отпугнут, лучше их на десерт. С принципом нарастания сложности полностью согласен. LGB 17:16, 16 февраля 2013 (UTC)
Иррациональные числа (как корни вещественных) и комплексные числа, как ещё более сложный случай таких корней[править код]
Есть ли работы, в которых комплексные числа предстают как дальнейшее развитие исследований, давших ранее иррациональные числа? Типа, были вот у греков целые числа, и даже культ целых чисел у пифагорейцев был, были отношения целых чисел - рациональные числа, затем они заметили что длина диагонали прямоугольного треугольника ни просто целым числом, ни даже их дробью не выражается - обнаружили иррациональные числа как корни. А затем вот изучая квадратные уравнения, обнаружили комплексные, как ещё более сложный вариант чисел, которые приходится уметь вычислять из несложных уравнений - многочленов - с обычными целыми числами в составе... --Nashev 11:35, 3 апреля 2013 (UTC)
- В рамках классической геометрии придти к понятию комплексного числа невозможно, оно там попросту не может возникнуть. КЧ — сугубо алгебраическое понятие, и возникло оно первоначально как вспомогательный, рабочий инструмент для нахождения вещественных корней неприводимого кубического уравнения (по формулам Кардано). Инструмент полезный, но сам по себе никому не нужный. Фактически только в посленьютоновский период, и особенно благодаря Эйлеру, КЧ изучаются уже как самостоятельный объект, обобщающий вещественные числа. LGB 11:49, 3 апреля 2013 (UTC)
- Неужто в аналитической геометрии не возникает квадратных уравнений с комплексными корнями? Я ж не говорю о классической, а говорю о её вполне возможном переосмыслении постфактум... --Nashev 13:00, 3 апреля 2013 (UTC)
И ещё: похоже, иррациональные числа по началу воспринимались такими же искусственно-сконструированными уродцами, не имеющими места в ряду чисел, как и сейчас ещё воспринимаются комплексные числа. А потом математики присмотрелись - и им нашлись промежутки на той же оси, прямо между последовательными рациональными, хоть их и бесконечно много. Ось стала ещё непрерывнее. Думаю, постепенно и комплексные числа должны уложиться в единую числовую ось как некое её целостное представление, но этому сильно мешает представление комплексных чисел в виде комбинации двух чисел, которое из одной линии числовой оси раскрывает в стороны от неё целую плоскость (хоть и одну). В этом месте мысли разбегаются:
- Кстати вот, рациональные дроби тоже имеют представление из двух чисел - геометрическая интерпретация рациональных дробей исследовалась?
- А кватернионы тоже как раскрытие новых свойств единой числовой оси можно считать? Типа, не одну плоскость вдоль оси развернули, а три?.. Или это ответвление в сторону от этой линии развития? Получаются ли кватернионы из выражений, содержащих лишь простые вещественные числа, как получаются комплексные числа? Или второе и последующие расширения процедурой Кэли — Диксона это уже действительно искусственные образования?
- И почему, собственно, всего одна плоскость развёрнута? В трёхмерном пространстве через прямую можно провести сколько угодно плоскостей, под разными углами к... как это назвать? во! к вертикали, если прямая горизонтальна, и аж две взаимно перпендикулярных, если учесть желательность независимости проекций точки этого пространства на эти плоскости. Да и кто сказал, что пространство вокруг прямой должно быть трёхмерно?..
- А вот такие вот дополнительные измерения для обычной одномерной числовой оси - это не те измерения, которые теория струн в нашем физическом пространстве находит? И свёрнутость тех измерений не аналогична фактическому отсутствию мнимого измерения комплексных чисел на одномерной числовой оси?
- Какое отношение имеет дополнительное мнимое измерение числовой оси к тем дополнительным дробным измерениям степени сложности структуры, которые вводятся теорией фрактальности?
Вот про всё тоже небось статьи и монографии есть, а? --Nashev 13:00, 3 апреля 2013 (UTC)
Экспонента в комплексной плоскости[править код]
Экспонента в комплексной плоскости проявляет периодичность - это неочевидное и важное свойство комплексных чисел. Где б в этой статье найти место, что бы это чудо упомянуть? --Nashev 21:56, 6 апреля 2013 (UTC)
- Разве в разделе "Тригонометрическая и показательная форма" недостаточно про комплексную экспонененту сказано? Или полезно разжевать для новичков?... И необязательно комплексная экспонента проявляет периодичность в комплексной плоскости, например, такая вычурная функция как exp(i*x + ln(1/sin(x))) = cos(x)/sin(x) + i не имеет периодичности по комплексной оси. С уважением, Д.Ильин 04:26, 7 апреля 2013 (UTC).
- Вот аналитические продолжения элементарных трансцендентных функций для комплексных аргументов и при
ОДЗОЗ недопустимой в вещественных числах (например, ln(x) при x<0) непременно надо бы описать. Если коллеги согласны с таким добавлением, я смогу сделать. Д.Ильин 04:49, 7 апреля 2013 (UTC).
- Вот аналитические продолжения элементарных трансцендентных функций для комплексных аргументов и при
- Я предлагаю вставить в конце раздел «Комплексные функции» (со ссылкой на Комплексный анализ как на главную статью), где вкратце объяснить, как получаются элементарные комплексные функции, чем они особенны и какая от них польза. LGB 10:31, 7 апреля 2013 (UTC)
- Коллега LGB, Ваше предложение продуктивно. Вы сами вставите "Коплексные функции", или мне? или другому сделать? По поводу полезности и применения - то в преамбулу, в расчетах, например, важных в практике функций Бесселя встречаются тригонометрические функции комплексного аргумента, в частности, в спектральном анализе частотно-модулированного синала. Д.Ильин 11:32, 7 апреля 2013 (UTC).
- У меня сейчас активность снижена, так что могу уступить место. LGB 11:52, 7 апреля 2013 (UTC)
- Статья, конечно, немного улучшена. Однако, хотелось бы узнать, не могла бы статья статья ещё лучше, если её перекомпоновать? Совершенно очевидно, что свойства различных комплексных функций (сами по себе достойные отдельной статьи) должны описываться в своём разделе, а различные формы представления числа — в своём. Всё-таки, сначала, нужно выбрать подходящую струкуру статьи, а уже потом дополнять её соответствующим текстом. --OZH 12:27, 25 апреля 2013 (UTC)
Физические интерпретации и толкования смысла[править код]
Нужен такой раздел, с перечнем реальных применений. Со ссылкой на комплексную амплитуду, волновую функцию и всё такое.
Думаю там же можно дать и толкование, что комплексная часть числа может отражать «напряжённость» или «плотность»,«давление», «запасёный потенциал» на соответствующем участке числовой оси. Если под эту интерпретацию АИ найдутся... --Nashev 09:54, 25 апреля 2013 (UTC)
- Впервые слышу, чтобы «напряжённость», «плотность», «давление», «запасённый потенциал» выражались комплексными числами. Мнимая часть обычно описывает «затухание».
- Обычно? В какой статье про это прочитать? В статье затухание нету... --Nashev 14:51, 25 апреля 2013 (UTC)
- Во всей изученной нами Вселенной не было обнаружено ни одного места, где физические величины, описывающие реальные явления, были бы комплексными. Количественные характеристики явлений нашего мира выражаются действительными числами. Вот вы можете представить улицу длинной (2+3i) метра? :))
- Но я знаю какой пример из физики можно привести. Как будет время, дополню этим статью. >> Kron7 10:39, 25 апреля 2013 (UTC)
- Спасибо, буду ждать и надеяться. --Nashev 14:51, 25 апреля 2013 (UTC)
график квадратного уравнения с комплексными корнями в комплексной плоскости[править код]
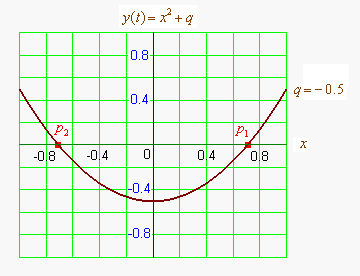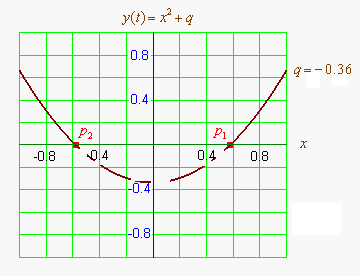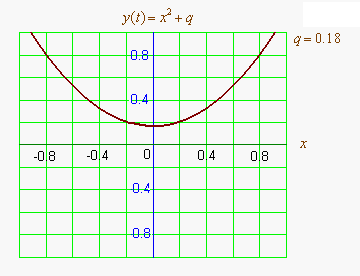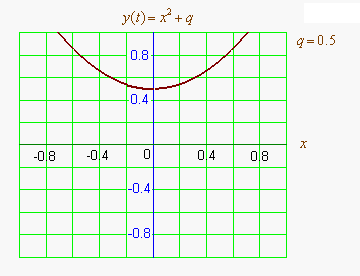
Или, иначе говоря, поверхность комплексной параболы, было бы полезно изобразить в изометрической проекции и добавить в статью. Может кто? --Nashev 11:01, 25 апреля 2013 (UTC)
- Коллега Nashev, я не понимаю термин "комплексная парабола", напишите формулу. Д.Ильин 12:55, 25 апреля 2013 (UTC).
- Я имел ввиду трёхмерный график функции . Видимо, его было бы удобно совместить с графиком (скажем, полупрозрачным) функции , и обозначить линию пересечения этих поверхностей — в общем, чтобы относительно наглядно были видны точки . --Nashev 14:51, 25 апреля 2013 (UTC)
- Теперь я понял, какое изображение Вы хотите видеть в статье. Его несложно создать даже в популярном Excel, не говоря уж о таких продвинутых программных пакетах как, скажем, Mathlab или MathCad. Но я не вижу целесообразности включения подобного рисунка в статью, так как не знаю значимости в приложениях. С уважением, Д.Ильин 16:45, 25 апреля 2013 (UTC).
- Наглядно представить те комплексные корни уравнения, которые появляются у квадратного уравнения при таком изменении коэффициентов, когда у него вещественные корни пропадают — думаю, должно быть очень полезным для их понимания. Так же, как чрезвычайно полезна для понимания вещественных корней картинка, где обычная двумерная парабола пересекает горизонтальную ось или касается её. --Nashev 17:13, 25 апреля 2013 (UTC)
- Все равно не понял, Вы хотите изобразить
полюсанули полинома a*x^2+b*x+с в комплексной плоскости, или поверхность модуля этого полинома при комплексном x (по оси z откладываем модуль). Тогда нужно придать разумные значения коэффициентом полинома. С уважением, Д.Ильин 08:10, 26 апреля 2013 (UTC).
- Все равно не понял, Вы хотите изобразить
- Я хочу в статье наглядно увидеть графики вещественной и мнимой частей функции и места их пересечения друг с другом и с нулевыми плоскостями. На графике с осями x, y в горизонтальной плоскости и z вверх. Заодно на этом графике можно будет наглядно увидеть, где находятся мнимые корни соответствующего квадратного уравнения — две точки на пересечениях обоих поверхностей друг с другом и с плоскостью z=0.
- Кстати, вещественная часть получается Гиперболическим параболоидом, мнимая — кажется, тоже он, но повёрнутый на 45 градусов.
- В Экселе попробовал — но он у меня не умеет две плоскости на одной диаграмме изобразить, да и непрезентабельно получается — только чтоб самому посмотреть, и то не всё увидишь… Matlab, MathCad, Wolfram и т.п. крутые пакеты мне неподручны пока. Вот Гугл нынче в результатах поиска симпатично рисует поверхности, если их просить по одной (вещественная z=x²-y²+1 и мнимая z=2*x*y), но отказывается рисовать их вместе, как он умеет рисовать двумерные графики, и к тому же обозначает пересечение лишь с горизонтальным нулём z=0, и нет возможности увидеть плоскость y=0. --Nashev 13:13, 26 апреля 2013 (UTC)
Выберу время, сделаю изображения 3D поверхностей, но с анимационным облетом, не как, в например, статическом 3D изображении модуля гамма-функции. Д.Ильин 21:58, 28 апреля 2013 (UTC).
- Коллега Nashev, что касается MathCad, или Wolfram, рекомендую изучить, много поможет. С уважением, Д.Ильин 22:13, 28 апреля 2013 (UTC).
Неравенство[править код]
Kron7 пишет: «Ошибка заключается в игнорировании приоритета операций: сначала должно осуществляться вычисление корня, а лишь потом умножение или возведение в степень». Это ошибка и чистой воды ВП:ОРИСС, приоритет здесь совершенно ни при чём. Напомню, что арифметический корень для отрицательного числа не имеет смысла. Если же понимать корень как алгебраический, то у него два значения, и в этом случае вся формула теряет смысл. Поэтому я убрал сбивающие с толку читателя пояснения. LGB 16:29, 17 мая 2013 (UTC)
- Итак
Kron7 пишет: «Ошибка заключается в игнорировании приоритета операций: сначала должно осуществляться вычисление корня, а лишь потом умножение или возведение в степень».
- Неужели я такое писал, вы ничего не путаете, уважаемый? >> Kron7 15:10, 23 мая 2013 (UTC)
- Ничего страшного, плохая память — явление распространённое. Это чья правка — см. тут ? Текст слегка отличается от позднейшей версии, но несущественно, ошибка та же. LGB 16:00, 23 мая 2013 (UTC)
- Уже на личности перешли)) Достойно;) >> Kron7 10:17, 24 мая 2013 (UTC)
- Текст кардинально отличается. Приоритет возведения в степень не зависит от значения показателя степени. По этому даже если распространенная ошибка, описанная в статье, имеет место не из-за нарушения приоритета операций, то он как минимум был правильно сформулирован («Сначала должно осуществляться поднесение к степени, а лишь потом умножение» - это истина), а в данном обсуждении вы процитировали товарища Nashev'а, который сказал: «Ошибка заключается в игнорировании приоритета операций: сначала должно осуществляться вычисление корня, а лишь потом умножение или возведение в степень». Извлечение корня и возведение в степень имеют одинаковый приоритет, а умножение и возведение в степень - разный. >> Kron7 10:17, 24 мая 2013 (UTC)
- Что такое поднесение к степени? Вы уверены, что это по-русски корректно? Я знаю "Возведение в степень", и подозревая, что Вы имели ввиду это, позволил себе подправить. Но тогда какой смысл сравнивать приоритеты операций "возведения в степень" и "умножения"? Особенно в контексте выражения, в котором противопоставляются вычисление корня возведению в степень? Подправил и это. Получилось то, что получилось. А что всё-таки имели ввиду Вы? --Nashev 10:46, 24 мая 2013 (UTC)
- Имелось ввиду возведение в степень. А на счет приоритета там оказался небольшой фейл - приоритет в статье не нарушается. >> Kron7 11:02, 24 мая 2013 (UTC)
- На будущее, LGB: ознакомьтесь с тем, что такое цитата - вам будет полезно. И не присваивайте одним людям - слова других, а то вы выставляете себя в дурном свете;) >> Kron7 10:17, 24 мая 2013 (UTC)
- Вы совершенно напрасно обиделись на безобидную шутку. Оба обсуждаемых текста едины в том, что во главу угла ставят приоритет операций, который с данной проблемой не имеет ни малейшей связи. Подробности ниже. LGB 11:21, 24 мая 2013 (UTC)
Напомню, что арифметический корень для отрицательного числа не имеет смысла. Если же понимать корень как алгебраический, то у него два значения, и в этом случае вся формула теряет смысл.
- Это вообще к чему? О какой формуле идет речь? >> Kron7 15:10, 23 мая 2013 (UTC)
- Именно та формула, которую вы выписали после заголовка. Если корень — двузначная функция, то непонятно, с каким значением левой части комбинировать правую часть (которая тоже неоднозначна). Ни один известный мне раздел математики с такими формулами не имеет дела. LGB 16:00, 23 мая 2013 (UTC)
- Ну посмотрим
Именно та формула, которую вы выписали после заголовка.
- Я вижу, вы очень сильны в мат. терминологии. То, что я указал в начале темы, называется «неравенство». Формула же должна содержать переменные. >> Kron7 10:17, 24 мая 2013 (UTC)
- А теперь посмотрите определение Математическая формула. В Мат. энциклопедии аналогично: «Формула есть выражение формализованного языка, предназначенное для записи суждения. Формула есть осмысленная комбинация символов.» В этом смысле выражение есть тоже формула, и она входит в некоторые аксиоматические системы как аксиома или теорема (в мат. логике любая теорема есть формула). LGB 11:21, 24 мая 2013 (UTC)
- Я вижу, вы очень сильны в мат. терминологии. То, что я указал в начале темы, называется «неравенство». Формула же должна содержать переменные. >> Kron7 10:17, 24 мая 2013 (UTC)
Если корень — двузначная функция, то непонятно, с каким значением левой части комбинировать правую часть (которая тоже неоднозначна).
- В целом справедливо, потому что правая часть имеет 2 значения, но вот вы опять делаете ошибки - левая однозначно определена: . Квадрат превращает (два значения) в (одно значение). >> Kron7 10:17, 24 мая 2013 (UTC)
- В любом случае, данное неравенство в статье неприменимо, я согласен. Но тем не менее в статье указано
- Корень в данном случае является алгебраическим, поскольку в первом выражении под ним находится отрицательное число. Тогда последний этап преобразований неверный, поскольку правильно . Следовательно
. - Тогда нужно добавить в статью. Но при этим все равно непонятно, почему такой ход решения неправильный. Об это см. далее. >> Kron7 10:17, 24 мая 2013 (UTC)
- Корень в данном случае является алгебраическим, поскольку в первом выражении под ним находится отрицательное число. Тогда последний этап преобразований неверный, поскольку правильно . Следовательно
Так в чем же ошибка?[править код]
Цитата из статьи:
Пример возможной ошибки при неосторожном использовании устаревшей записи:
При использовании современной записи такой ошибки не возникло бы:
Если добавить в первую цепочку вычислений знак и получить
то в чем же будет ошибка? >> Kron7 10:17, 24 мая 2013 (UTC)
- Дело вот в чём. Существуют два определения корня: арифметический и общеалгебраический (см. Мат. энциклопедию). В формулах (и ваших, и переделанных Nashev) неявно используется третье, никаким источником не подтверждаемое, определение:
- для неотрицательных чисел корень арифметический;
- для отрицательных чисел
- Если не согласны, приведите собственное определение однозначного корня из отрицательного числа.
- Но тогда легко убедиться, что для такого определения правило: не выполняется, и пользоваться им нельзя. Все приведенные рассуждения теряют смысл. LGB 11:22, 24 мая 2013 (UTC)
- Немного переформулируем (см. раздел Обсуждение:Корень (математика)#Алгебраический корень и арифметический корень). >> Kron7 11:44, 28 мая 2013 (UTC)
Не пора ли номинировать[править код]
На какой-нибудь статус, типа хорошая или избранная? Вроде, статья нынче неплохая (если не считать этого примечания, о котором спор чуть выше вышел).. --Nashev 13:52, 24 мая 2013 (UTC)
- Мне кажется, ещё рано. Посмотрите на английскую статью — там обширный раздел о применениях (Applications), есть немного об анализе, все модели, как я предлагал, перенесены в конец (Formal construction), история более содержательная, для продвинутых описаны тонкие алгебраические и топологические свойства и т. п. Я планирую в июне существенно дополнить нашу статью, в том числе взяв всё лучшее из английской. Тогда, может быть, и на избранную потянет. Надеюсь на ваше соучастие. LGB 15:41, 24 мая 2013 (UTC)
- Да, английский вариант лучше, но и выглядит некоторым нагромождением. Нам следует бороться за связность изложения, а что-то как бы вдруг ниоткуда возникает и в никуда уходит. Для алгебраического аспекта комплексных чисел было бы удобно иметь статью «Поле комплексных чисел», а статью «Комплексные числа» я бы сделал большим обзором того, что такое КЧ и с чем их едят, и где потребляют. Ну а совсем лично и совсем субъективно, я бы сделал отдельную статью «Комплексное число» с описанием различных форм представления комплексных чисел. --OZH 12:03, 31 мая 2013 (UTC)
Пора номинировать на золотую малину[править код]
- Статья - отстой. Чтобы понять то, что в ней написано, требуется искать ещё информацию _по теме_, именно по комплексным числам, вне статьи. 109.161.88.33 16:31, 20 августа 2013 (UTC)
Правки Tosha[править код]
Я откатил с пояснением «Это ж надо, так поломать починенную статью! В обсуждение сначала, плиз, обоснования.». Прошу объясниться, прежде чем пытаться их повторять. --Nashev 10:16, 7 июля 2013 (UTC)
- Во первых преамбула должна быть более элементарной --- термины поле и расширение здесь не нужно использовать, те кто знает что такое поле не будут смотреть эту статью.
- Во вторых то что сейчас называется «определением» определением НЕ является, это только разговоры на тему.
- Остальные мои правки мелкие но тоже могу обосновать если потребуется.
- Откатываю --Тоша 19:04, 2 августа 2013 (UTC)
- Я согласен, что слово «поле» не обязательно упоминать в преамбуле. Но я не вижу в нём ничего настолько ужасного, чтобы не определить его ближе к концу статьи. Например, в начале раздела «Свойства» было бы естественно написать, что сложение коммутативно и т. д., поэтому комплексные числа образуют поле. Даже в статье «рациональные числа» это упоминается; к тому же в этой статье сейчас пару раз употребляется слово поле (даже без ссылки), люди ведь могут неправильно понять это слово :). Danneks 04:53, 3 августа 2013 (UTC)
- Ну, начнём с того, что вид «x+iy, где x и y — вещественные числа, i — мнимая единица;» — это не единственное и не главное представление комплексных чисел. Более того, совершенно не принципиальное. Представлений у комплексных чисел штук пять разных, и по большому счёту все равноценны. Некоторые из них даже мнимой единицы не содержат! Единственное, что эти числа действительно характеризует — это что при возведении некоторых из них в квадрат может получиться отрицательное вещественное число. Преамбула должна говорить об этом, о главном, а формы нужно вводить ниже по тексту, что и было Вами поломано. Остальные мелкие правки тоже обсудим, ибо практически все они на мой взгляд тоже вредны. Что касается слова "поля" - уверен, что незнакомые с терминологией вполне способны догадаться, что "поле вещественных чисел" это чуть более строгая формулировка для "множества вещественных чисел", и если хочется - полезут в тонкости, но могут и не захотеть. Убедил? --Nashev 16:19, 5 августа 2013 (UTC)
- Уважаемые коллеги, хочу напомнить, что в Википедии всё решают источники. В математической энциклопедии определение такое:
Комплексное число — число вида , где — действительные числа, а — так называемая мнимая единица, то есть число, квадрат которого равен (в технической литературе применяется также обозначение ).
- Предлагаю принять в целом. Заодно пара замечаний.
- 1. Утверждение о том, что идея комплексного числа возникла в результате формального решения квадратных (а не кубических) уравнений, ошибочно, см. исторический очерк. До формул Кардано никому и в голову не приходило, что квадратные корни из отрицательных чисел могут принести какую-либо практическую пользу.
- 2. Требование Tosha исключить понятие алгебраического поля из начала статьи всецело поддерживаю. Данную статью читают преимущественно школьники, и этот факт должен быть отражён в её построении — весь материал, выходящий за школьный уровень, должен быть расположен ближе к концу текста. В будущем разделе «Определение» можно кратко пояснить простыми словами, как происходит расширение вещественных чисел до комплексных, включая операции с ними. LGB 16:45, 5 августа 2013 (UTC)
- По первому замечанию, цитирую первое же предложение раздела «История»: "Впервые, по-видимому, мнимые величины были упомянуты в известном труде «Великое искусство, или об алгебраических правилах» Кардано (1545), в рамках формального решения задачи по вычислению двух чисел, которые в сумме дают 10, а при перемножении дают 40. " — это разве не формальное решение квадратного уравнения и не возникновение идеи комплексного числа? --Nashev 18:08, 6 августа 2013 (UTC)
- До открытия формул Кардано никто — подчёркиваю, никто — не обращал внимания на комплексные корни квадратных уравнений, хотя эти уравнения умели решать ещё шумеры и вавилоняне. Сам Кардано, очевидно, тоже заинтересовался квадратными корнями из отрицательных чисел при исследовании формул Кардано. Причём комплексное решение он считал бесполезным и признаком того, что задача неразрешима. Настоящее применение комплексных чисел начинается с Бомбелли, см. Историю математики Юшкевича. Таким образом, источником теории являются кубические уравнения. LGB 11:07, 7 августа 2013 (UTC)
- По остальным возражениям — не согласен, но бессилен (АИ, дающих комплексные числа корректно, не знаю), умываю руки и включаю режим вики-ленивца. Хотя, напоследок возражу, что именно школьникам полезно понимать, что форма x+iy — не самое не главное в комплексном числе. Про то, что слово «поле» не страшно — я уже писал. Проигнорировали. --Nashev 18:08, 6 августа 2013 (UTC)
- А что, собственно, мешает в преамбуле совместить формальный и методико-преподавательский подход в определении комплексных чисел?
Комплексные числа — расширение поля вещественных чисел. Проще говоря, это числа, которые можно представить в виде , где и — вещественные числа, — мнимая единица.
- Ну или начать со «школьного» определения, а следующим предложением ввести математически корректное.
- PS. Удивляет разнообразие подходов к написанию разных статей: то Википедия — это энциклопедия (с вытекающим из этого требованием к подготовке читающего), то вдруг начинается «буча», что Вики, мол-де, это для «детишек-дошколят». Тут нужно раз и навсегда определиться со стилем статей. Что должно превалировать: «взрослые» (научно-популярные, направленные на подготовленного читателя) или «детско-юношеские» (не всегда корректные, но зато понятные простому читателю). Также никто не запрещает подойти диалектически и писать в преамбуле на доступном языке, а далее давать конкретный научный материал. Кому надо — будет разбираться и поймёт на доступном для себя уровне. Если уж в стране все виды образования в ауте, то уж хотя бы здесь-то «истинное» знание должно же остаться. — KleverI 20:35, 6 августа 2013 (UTC)
- Давайте разберёмся, кто будет читать статью о комплексных числах. Тот, кому известно понятие «расширение поля», уж точно читать не будет. Общее правило: любая научная статья должна быть рассчитана на читателя с подготовкой, минимально необходимой для понимания основной части статьи. Это не значит, что все статьи должны содержать только школьный материал, но и другая крайность столь же вредна. Конечно, есть статьи для узкого круга, но Комплексное число — явно не из этой категории.
- Оптимальный вариант любой научной статьи: основная часть должна включать содержательный и понятный обзор материала, а в конце размещается информация для более продвинутых читателей. Вот и всё, казалось бы, все должны с этим согласиться, но почему-то постоянно возникают бессмысленные споры, а часть статей по математике демонстрируют откровенный выпендрёж: «вот какие я умные слова знаю!» Посмотрите, например, статьи Дифференциальный оператор или Конформное отображение — это же важнейшие темы, у них должны быть сотни читателей в день, а в реальности — в лучшем случае десяток, и те уходят разочарованными. Потому что вместо информации там выпендрёж, сравните с аналогами в английской Вики. Чем раньше участник поймёт, что пишет не для себя, а для массового читателя, тем больше пользы принесут его статьи. Снобизм тут не к месту. Извините, никого не хотел обидеть. LGB 11:07, 7 августа 2013 (UTC)
- Обсуждения целевой аудитории лучше вести в контексте проекта правила ВП:ПРОЩЕ. В любом случае, упрощение подачи материала не должно приводить к понижению его качества (достоверности и полноты). И вещи, описанные понятными словами, назвать ещё и правильными словами - тоже полезно. Если правильные слова достаточно понятны сами по себе - то можно и сразу ими. Слово "поле" - ИМХО, достаточно понятно. --Nashev 12:18, 7 августа 2013 (UTC)
- Если в первую очередь опираться на уровень школьной программы, то понятие «поле» в школе не рассматривается. Данный термин впервые встретится человеку (учитывая, что он не будет искать об этом инф самостоятельно) лишь в ВУЗе на математической специальности (даже не все физ-мат специальности изучают «поле», поскольку физикам в большей степени это ни к чему). >> Kron7 12:49, 7 августа 2013 (UTC)
- Поле — абстрактное понятие (обобщение свойств других объектов), оно будет понятно, если есть достаточная мотивация для того, чтобы его понять. Если же человек не знает, что такое комплексные числа (Вы согласны, что начало статьи должно быть построено с расчётом на таких читателей?), то он вряд ли захочет вникать в определение поля. Danneks 13:10, 7 августа 2013 (UTC)
Мнение ещё одного участника[править код]
Нет культурных слов. Русская(tm) Вики(r)педия(tm) превращается незнамо во что. Мало того, что статья отвратительна, как и абсолютное большинство русских статей в википедии по математике и физике, так теперь ещё и отключили возможность правки. И это ещё хотят на что-то "номинировать"?! Серьёзно? Посмотрите хотя бы английскую статью перед тем, как что-то писать: всё чётко, подробно объяснено, картинки вынесены в начало, материал подан последовательно. На кого расчитана эта статья? На школьников или студентов первого курса? Не похоже. Объяснено так, будто "очевидно, что" человек должен это знать. Но те, кто знают, не будут читать эту статью.
И по теме. Где вывод деления комплексных чисел? Вы считаете, что формула очевидна? И уберите тему "Связанные определения". "Модуль комплексного числа" не существует без "комплексного числа". Зачем засовывать его в середину под непонятный заголовок? Введите понятие сопряжённого числа перед действиями над числами. Покажите вывод всех формул, включая деление. И перенесите геометрическую модель в начало. Хотя бы перед матричной. "Представления комплексных чисел" тоже неплохо бы сократить и перенести ближе к началу. 109.161.88.33 16:44, 20 августа 2013 (UTC)
- Успокойтесь, ничего ужасного не происходит (первый параграф излишний). Вывод деления добавил, это не трудно. Не вижу ничего ужасного в слове «Связанные определения», они на то и связаны, что не существуют без основной темы (а вот определение комплексного числа существует и без определения модуля). Не знаю, что вы подразумеваете под выводом всех формул в статье, вывод из аксиом? :) Можете зарегистрироваться и заняться этим. Параграф «геометрическая модель» целиком переносить в начало нельзя, так как в нём даётся интерпретация введённых ранее операций. И непонятно, в какое место статьи вы собираетесь переносить представления — переносить тригонометрическое представление раньше определения аргумента нельзя. Danneks 06:46, 21 августа 2013 (UTC)
- "Ужасного" действительно ничего не происходит. Просто кажется больш`ая часть статей по сходной тематике написана авторами для себя.
- Открывая статью, впадаешь в ступор от обилия непонятных очевидностей. А, пролистывая английские статьи удивляешься, что не так всё и сложно...
- Как в бородатом анекдоте про отличия английского, еврейского и русского форумов.
- 1. Формально, вы правы насчёт "связанных определений". Но то же самое понятие модуля широко используется и достаточно просто для введения в начале.
- А заголовок излишен.
- 2. Вывод всех формул, которые не являются аксиомами. И, в рамках разумного, объяснение "аксиом".
- Так конечно: не выведено деление (совсем не очевидно, что нужно домножить дробь на сопряжённое знаменателя), понятие модуля введено где-то в центре статьи,
- изредка проскакивает "Ландавшиц-стайл" и т.д... Сущие мелочи. В итоге, статья становится непонятна и тяжело читаема: "Дьявол в деталях".
- 3. Понятие "наглядность" отражает то, что многим людям объяснение понятнее, когда они глядят на картинку.
- "Геометрическая модель" - это картинка. Взгляд на картинку (если её возможно построить) даёт большинству людей более чёткое представление о предмете.
- Зачем человеку читать нечто сложное о неком "семействе вещественных матриц", которое стоит ранее геометрической модели, когда он не представляет, что такое комплексное число и с чем его едят?
- По-моему, здесь есть некое нарушение "принципа нарастания сложности".
- И я считаю, что правильно написано в английской статье: краткое определение и очень краткая история в шапке, картинка в верхнем правом углу, в подписи картинки сжатое описание геометричекого представления.
- Заметьте, что операции в их статье даются также с их визуальным представлением.
- 4. Зачем регистрироваться, когда предполагается, что энциколпедию может править каждый? :-\
109.161.82.4 18:39, 21 августа 2013 (UTC)
- Нет ничего удивительного в том, что в английской Википедии многие темы объяснены лучше — всё-таки в ней в 12 раз больше активных участников, статьи на основные интересные темы уже написаны и остаётся только улучшать уже имеющиеся. Я не против переноса текстов из англовики (я сам практически только этим и занимаюсь), но в данном случае, наверно, другие авторы статьи будут против. Согласитесь, что в статье уже есть самая базовая информация по теме, а понятность изложения будет, когда кто-то захочет этим заняться (можете ещё посмотреть Википедия:Отказ от ответственности). Если Вы про слова «которую может редактировать каждый» на главной странице, то если пройти по ссылке, там вроде бы всё правильно написано. Danneks 05:04, 22 августа 2013 (UTC)
- Я не агитирую за бездумный перенос текста откуда-либо. Но это не значит, что не нужно смотреть на пример того, что лучше (будь это не англйская, а хоть китайская или чеченская вики :-\ ).
- Я согласен, что в данной статье достаточно много написано грамотно и по теме и не призываю до основания всё разрушить, заменив переводом.
- И да, я про слова "может редактировать каждый" и запрет на редактирование статей, в том числе. Сначала закрывают Tor, потом ненавязчиво статьи, "предлагая" "свободную" регистрацию,
- потом "неполиткорректные выссказывания", потом...
- Очень в духе РФ. 87.253.19.234 15:50, 22 августа 2013 (UTC)
- Защищена статья была когда-то от слишком активных несогласованных правок анонимами. Неанонимного участника можно пытаться урезонить персонально, он как правило дорожит своим именем, поэтому им правки разрешены. Через некоторое время, когда теоретически конфликтующим анонимам надоест ждать и пропадёт желание раздирать статью на свой вкус, защита должна быть снята. Это вполне резонная практика... Правда, пора снять уже, думаю... Кто тут права на это имеет? Ау! --Nashev 15:23, 2 сентября 2013 (UTC)
- Нет ничего удивительного в том, что в английской Википедии многие темы объяснены лучше — всё-таки в ней в 12 раз больше активных участников, статьи на основные интересные темы уже написаны и остаётся только улучшать уже имеющиеся. Я не против переноса текстов из англовики (я сам практически только этим и занимаюсь), но в данном случае, наверно, другие авторы статьи будут против. Согласитесь, что в статье уже есть самая базовая информация по теме, а понятность изложения будет, когда кто-то захочет этим заняться (можете ещё посмотреть Википедия:Отказ от ответственности). Если Вы про слова «которую может редактировать каждый» на главной странице, то если пройти по ссылке, там вроде бы всё правильно написано. Danneks 05:04, 22 августа 2013 (UTC)
- Вас, как новое заинтересованное лицо, я прошу высказаться по варианту структуры статьи, который я предлагал некоторое время назад я, и которую начинали было обсуждать в разделе "Правки Tosha" --Nashev 15:23, 2 сентября 2013 (UTC)
- Мне кажется не стоит снимать защиту. "Активные несогласованные правки анонимами" приходят волнами ежегодно; они вероятно совпадают с началом изучения комплексных чисел в проф. тех. училищах. --Тоша 00:44, 3 сентября 2013 (UTC)
Сообщение об ошибке[править код]
В замечаниях там будет не 3, а +-3. Автор сообщения: 176.51.6.134 12:50, 16 сентября 2013 (UTC)
- Ошибки вроде нет, а вроде и есть. +- я считаю более корректно будет, поэтому исправлю. Ery 14:38, 16 сентября 2013 (UTC)
- Никаких оснований для плюс-минуса нет. Речь идёт просто о замене старой записи на более корректную, оба способа записи предполагали однозначное истолкование, в то время как плюс-минус даёт двузначное. Если не согласны, выходите на страницу обсуждения статьи. LGB 16:22, 16 сентября 2013 (UTC)
![]() К обсуждению--Draa kul talk 16:31, 16 сентября 2013 (UTC)
К обсуждению--Draa kul talk 16:31, 16 сентября 2013 (UTC)
- Тут как я понял проблема с обозначением корня. Подразумевается арифметический, однако из-за наличия отрицательного числа под ним воспринимается как алгебраический, отсюда и +-. Меня это именно и смутило. Ery 17:01, 16 сентября 2013 (UTC)
- Прочитал, это уже обсуждалось выше. Оказывается не я один на это попался. Ery 17:09, 16 сентября 2013 (UTC)
- Да, верно, арифметический корень по определению имеет смысл только для неотрицательных чисел. Старый формат записи мнимого числа вроде по смыслу точно соответствует современному в статье объясняется, почему старый формат был заменён (провоцировал возможные ошибки пользователя). LGB 17:14, 16 сентября 2013 (UTC)
Корень квадратный из комплексного числа[править код]
Не стоит ли добавить способ извлечения квадратного корня: (a+bi)^0.5 = c + di, где c и d даются системой уравнений a = c^2 - d^2; b = 2cd;
?
195.70.217.10 13:52, 30 октября 2013 (UTC) юзер
- Ну и в чём конкретно состоит этот способ? И чем он лучше тригонометрического? LGB 15:26, 30 октября 2013 (UTC)
Орфография и пунктуация[править код]
Предлагаю в этой теме обсуждать неточности и орфографические ошибки в тексте.
Сопряжённые числа[править код]
Ниже предложение из этого раздела, смысл которого мне не понятен. Много несогласованных слов в предложении. Правильный вариант предложить не могу, поскольку я сам читаю эту статью, чтобы вспомнить курс математики. Возможно, стоит как-нибудь разбить его на два предложения.
Произведение комплексно-сопряженных чисел важно в квантовой механике, не имеющая физического смысла комплексная волновая функция, исчерпывающе описывающую систему микрочастиц, будучи умноженная на своё комплексное сопряжение даёт имеющую физический смысл плотность вероятности нахождения частицы в рассматриваемой точке.
Вот в этом предложении исправил.
Умножение числителя и знаменателя комплексной дроби при комплексном знаменателе на сопряжённое к знаменателю выражение используется для устранения комплексности знаменателя, что позволяет представить выражение в канонической форме комплексного числа или функции.
Тут тоже не очень понятно с корнями.
Алгебраический многочлен с вещественными коэффициентами всегда имеет либо только действительные корни, если он ещё или только имеет комплексные корни, то комплексные корни всегда попарно комплексно сопряжены.
Формула Муавра и извлечение корней из комплексных чисел[править код]
где r — модуль, а \varphi — аргумент комплексного числа. В современной символике она опубликована Эйлером в 1722 году. Приведенная формула справедлива при любом целом n, не обязательно положительном.
Может, где-то ещё есть, исправьте, пожалуйста. 91.204.166.54 07:35, 16 апреля 2014 (UTC)
Так же как[править код]
ТАК ЖЕ(,) КАК (И), союз; наречие + частица + союз
1. Союз. То же, что «равно как (и)». Синтаксические конструкции с союзом «так же как (и)» выделяются знаками препинания (запятыми). Между частями союза знаки препинания не требуются.
Так же как в средневековой харчевне, нас встречали дома бревенчатые темные стены, законопаченные желтым мхом, пылающие поленья в печке и запах тмина. К. Паустовский, Бакенщик. Я знала, так же как и она, что рано или поздно наступит день, когда мы поневоле заговорим и простим друг другу долгое молчание. Ч. Айтматов, Материнское поле.
2. Наречие + частица + союз. Запятая ставится перед словом «как».
От тяжелой росистой травы кругом и от цветов, ночных цветов, только теперь раскрывших свои головки, пахло так же, как от волос Анны. С. Сергеев-Ценский, Печаль полей. Совершенно так же, как в жмурках, бывало мы, ребята, шли с завязанными глазами, так и она переступала с лапки на лапку в направлении леса. М. Пришвин, Охотничьи собаки.
2A00:1370:8130:A72:4060:B857:2F7E:48B6 13:30, 16 июня 2016 (UTC)
Для комплексных чисел операции также (тоже) определены. Но определены они не так, как для вещественных, а по-другому. 2A00:1370:8130:A72:4060:B857:2F7E:48B6 13:32, 16 июня 2016 (UTC)










































































